DFS (Depth First Search) 깊이 우선 탐색

이론 핵심 요약

그림 출처

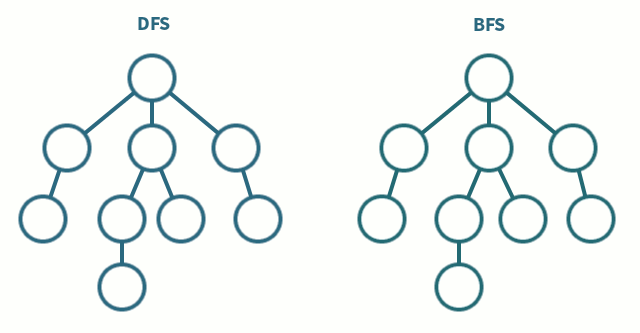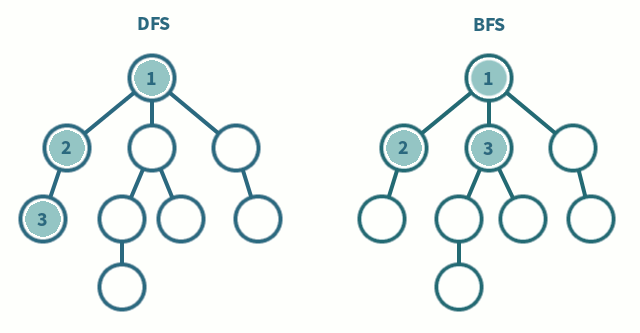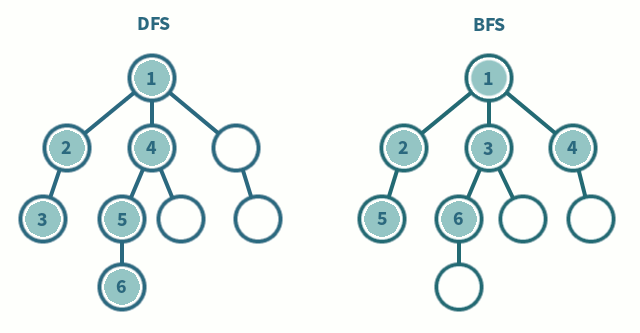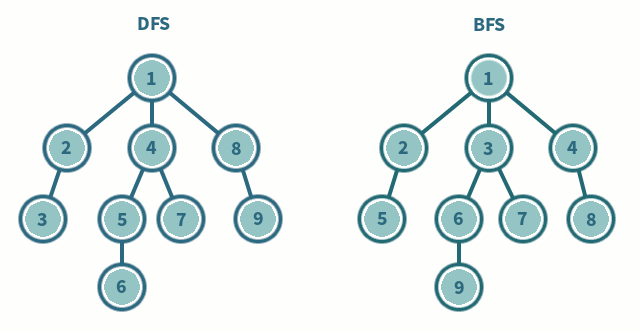
• 탐색 알고리즘
  • 그래프나, 트리에서 존재하는 모든 노드를 방문(탐색) 하는 방법의 하나
  • DFS는 한 루트에서, 최대한 깊숙히 들어가서 확인하고, 다시 돌아가서 다른 루트로 탐색하는 방법
  • 백트래킹 (모든 경우 검사) 에서 사용 가능
  • 복잡도 O(V^2)
    • 최악의 경우 V^2의 복잡도.
    • 가지치기를 이용해서 잘라내기를 하면, 해당 노드의 자식이 모두 잘라지는 효과 있음 (복잡도를 줄일 수 있음)
    • 그래프의 표현을 인접 행렬 O(V^2) 대신, 인접 리스트 사용시 O(V + E)로 줄일 수 있다.
      • V: 정점(Vector), E: 간선(Edge)
  • 주의
    • 재귀호출 사용시, stack overflow 주의 필요.
    • stack을 직접 사용하는 형태로, 변경 가능

구현 핵심 요약

Java로 설명한다.

필요한 요소

• 그래프를 표현한 자료구조 (ArrayList | Array [][])
• 방문 정보를 기록하기위한 테이블 (int visted[])

코드

인접행렬

public boolean[] visited;
public int[][] graph;

public void dfs(int node) { // node == node index
    visited[node] = true;

    for (int i = 0; i < graph[node].length; i++) {
        if (graph[node][i] == 1 && visited[i] == false) {
            dfs(i);
        }
    }
}

// 그래프가 disconnected 이거나 방향그래프여서 모든 노드가 방문 불가능할때, 모든 노드 방문 시키기
public void dfsAll() {
    for (int i = 0; i < graph.length; i++) {
        if (visited[i] == false) {
            dfs(i);
        }
    }
}

• 출발점이 정해져 있으면, dfs(출발 index)로 그냥 호출하면됨.
• 그래프와 같이 여러 출발점이 있을 수 있는 경우, visited가 되지 않은 출발점으로 부터 다시 dfs을 호출하도록 해야 모든 노드 탐색이 가능

인접리스트

public boolean[] visited;
public ArrayList<ArrayList<Integer>> graph;

public void dfs(int node) { // node == node index
    visited[node] = true;

    ArrayList<Integer> connectNodeList = graph.get(node);
    for (int i = 0; i < connectNodeList.size(); i++) {
        int connectNode = connectNodeList.get(i);
        if (visited[connectNode] == false) {
            dfs(connectNode);
        }
    }
}

public void dfsSimple(int node) { // node == node index
    visited[node] = true;

    for (int connectNode: graph.get(node)) { // graph.get(node) => ArrayList가 나오고 이걸 for로 돔.
        if (visited[connectNode] == false) {
            dfs(connectNode);
        }
    }
}

// 그래프가 disconnected 이거나 방향그래프여서 모든 노드가 방문 불가능할때, 모든 노드 방문 시키기
public void dfsAll() {
    for (int i = 0; i < graph.length; i++) {
        if (visited[i] == false) {
            dfs(i);
        }
    }
}

의사코드

// DFS 깊이 우선탐색
DFS(G, v)
    visited[v] <= YES;
    for each node u adjacent to v do
        if visited[u] = NO then
            DFS(G, u)
    end.
end.