세그먼트 트리(Segment Tree)

기본 개념 정리

일반적인 트리의 node들이 어떤 값이나 객체를 나타내는 것과 달리, 트리의 node들이 범위을 나타내고 있는 경우, 이를 세그먼트 트리 라고 한다.

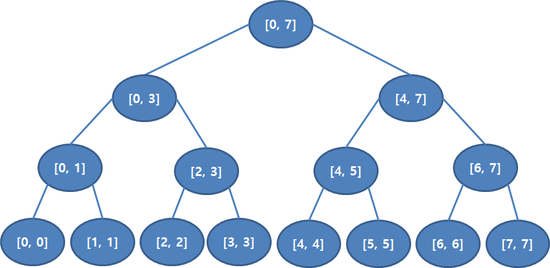
그림 출처: http://blog.naver.com/PostView.nhn?blogId=kks227&logNo=220791986409

예를 들어 어떤 아이템이 0 ~ 7 까지 있다고 가정하자. 그리고 해당 아이템을 구간(범위) 별로 더한 값이 필요하다고 가정하자.

이때, 구간이 랜덤하게 주어졌을때, 해당 구간의 값을 구하려면, 항상 구간을 자르고, 해당 구간만큼 더하는 연산이 필요하다.

하지만 위와 같이 세그먼트 트리를 구성하면, 랜덤한 구간이 주어졌을때, 해당 구간에 대한 값을 바로 가져올 수 있다.

세그먼트 트리의 핵심은, 트리의 노드가 구간을 의미 (혹은 해당 구간 만큼의 값을 의미) 한다는 점이다.

이론 핵심 요약

어떤 구간의 값을 나타내는 알고리즘
- 트리의 요소 (Item)은 정해져 있고, 해당 요소의 범위(구간)에 대한 값(합, 차, 최소, 최대, 평균, .. 등등)을 구할 때 사용
- 트리를 완전 이진 트리(포화 이진트리) 형태로 만들어서 풀이한다.
  - 트리의 요소 (Item)는 2^a (2의 a 승) 형태로 처리 한다.
  - 만약 2^a승 형태가 아닌 경우, dummy을 주어서 항상 2^a인 형태로 처리한다.
- 트리의 요소가 2^a승 형태가 아닌 경우, HashMap와 같은 자료구조를 사용해서 처리해도 답을 도출 할 수 있다. 다만 array형태를 사용하고 dummy을 주어서 처리하는 것 보다, 속도가 느리다.
- 세그먼트 트리의 노드는 Level순회 형태로 ID를 부여한다.
- 세그먼트 트리의 마지막 Leaf노드는 범위가 자기자신인 형태가 된다.
- 복잡도 O(Log N)
  - 알고리즘 자체가 logN 의 범주로 되어 있다.(완전 이진 트리로 봤을때, 깊이는 logN이되고, left자식, right자식, 을 방문하는 형태를 취하면, 2LogN 의 복잡도가 나온다)

구현 핵심 요약

Java로 설명한다.

필요한 요소

문제에서 주어지는 Item을 저장하는 자료구조 (Array | List) - e.g) int [] items
세그먼트 트리를 표현하는 자료구조 (Array | HashMap) - e.g) int [] tree
세그먼트 트리의 크기를 계산하는 함수
세그먼트 트리를 생성하는 함수
세그먼트 트리를 방문(답을 구하는)하는 함수

코드

세그먼트 트리의 크기를 계산하는 함수

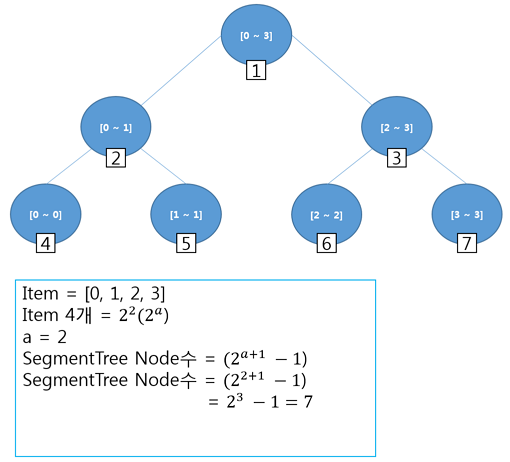
세그먼트 트리의 크기 (전체 노드 수)는, 문제에서 주어진 Item이 2^a승 형태일 경우 2^(a + 1) -1 이다.
- e.g) Item이 4개라고한다면, 2^2승 형태가 된다. 따라서 a== 2가 된다. 위 공식에 따라서 2^(a + 1) -1 == 2^(2 + 1) -1 == 2^3 - 1 이 된다.
- 2^3 -1(2의 3승 - 1) == 7

결과적으로 2^3-1은(2의 3승 -1) == 7 이 된다.

문제에서 주어진 Item이 2^a승 형태가 아닌 경우 2^a 형태로 만들어야 한다. 즉 주어진 Item숫자를 가지고 가장근접한 2^a을 만들어야 한다.
- 예를 들어 Item의 전체 갯수가 9 인 경우, 가장 근접한 2^a는 16(a == 4) 이다.
- 주어진 숫자를 X라고 했을때, 가장 근접한 2^a 을 찾으려면, X를 log2(X) 로 만들면 된다.
- Java에는 log2가 없기 때문에 logX / log 2을 하면 log2(X)가 된다.

a 구하기

// 2의 a승 형태로 만들기 (다시 말해서 a 구하기)
public static int log2(int x) {
    // 아래 계산의 의미
    // 예를 들어 x == 9라고 햇을때 아래의 식은
    // 3 < 3 + log2 < 4 를 의미한다.
    Double result = Math.log(x) / Math.log(2);

    return result.intValue() + 1;
}

어떤 수를 2^a 형태로 만드는 간단한 방법이 있다. 어떤 수에 4를 곱하면 된다.
- 왜냐하면 2의 제곱수를 곱하여 나온 수는 항상 2의 제곱수가 된다. 따라서, 2^a형태가 된다.

트리의 크기 구하기

public static int tree[];

// 2의 a승 형태로 만들기 (다시 말해서 a 구하기)
public static int log2(int x) {
    // 아래 계산의 의미
    // 예를 들어 x == 9라고 햇을때 아래의 식은
    // 3 < 3 + log2 < 4 를 의미한다.
    Double result = Math.log(x) / Math.log(2);

    return result.intValue() + 1;
}

// 트리 초기화
public static void initTree() {
    // 2^(a + 1) - 1
    Double len = Math.pow(2, log2(ItemTotalNumber) + 1) - 1;
    tree = new int[len.intValue()];
}

// 2^a 을 구하지 않고 4를 곱해서 바로 트리 초기화 하는 경우
public static void initTree() {
    tree = new int[ItemTotalNumber * 4];
}

위에서 설명한 a는 segment tree의 depth(height)가 된다.

곱하기 4를 하는 경우, 메모리 낭비 문제가 발생한다. 문제에 따라 적용하면된다.

세그먼트 트리를 생성하는 함수

트리의 생성은 간단하다, 트리 노드가 Leaf면 자기 값을 트리에 저장하고, Leaf가 아니면, 왼쪽, 오른쪽 노드 값을 계산한 이후 저장하는 형태를 취하면 된다.

// 예제에서는 sum을 가정하였음.(구간의 합을 세그먼트 트리가 저장하고 있다고 가정)
public static int createTree(int nodeId, int L, int R) {
    // Leaf 노드면
    if (L == R) {
        tree[nodeId] = itemList[L];
        return tree[nodeId];
    } else {
    // Leaf 노드가 아니면, 왼쪽, 오른쪽 자식을 가져와서 계산
    // nodeID는 level 순회 형태로 표기
    // leftChild ID = (nodeId * 2)
    // rightChild ID = (nodeId * 2) + 1
        int mid = (L + R) / 2;
        int leftTreeSum = createTree(nodeId * 2, L, mid);
        int rightTreeSum = createTree(nodeId * 2 + 1, mid + 1, R);

        tree[nodeId] = leftTreeSum + rightTreeSum;
        return tree[nodeId];
    }
}

문제가 주어졌을때, 세그먼트 트리를 생성해두면, 이후 구간이 주어졌을때, logN 의 시간 복잡도로 답이 나오게 된다.

세그먼트 트리를 방문(답을 구하는)하는 함수

// 예제에서는 구간의 sum을 가정함
public static int segmentTree(int L, int R, int nodeId, int nodeL, int nodeR) {
    // [구하려는 범위], [현재 노드 범위], [구하려는 범위]
    // 구하려는 범위가 현재 노드 범위 전체의 왼쪽 범위, 또는 오른쪽 범위로, 완전 벋어나져 있는 경우
    // 현재 노드에서는 구할 수 있는 값이 없음.
    if (R < nodeL || L > nodeR) {
        // sum 에서 0은 null과 마찬가지로 영향을 주지 않으니깐 0 리턴
        return 0;
    }

    // [구하려는 ..., [현재 노드 범위], ... 범위]
    // 현재 노드 범위 전체가, 구하려는 범위 안에 속하면, 현재 노드 범위의 값을 리턴
    if (L <= nodeL && R >= nodeR) {
        return tree[nodeId];
    }

    // 구하려는 범위 나머지를 구해야 함. (구하려는 범위가 현재 노드 범위에 걸쳐 있는 경우임)
    int mid = (nodeL + nodeR)/2;
    int sumL = segmentTree(L, R, nodeId * 2, nodeL, mid);
    int sumR = segmentTree(L, R, (nodeId * 2) + 1, mid + 1, nodeR);

    return sumL + sumR;
}

L: 구하고자 하는 범위의 맨 왼쪽
R: 구하고자 하는 범위의 맨 오른쪽
nodeId: 현재 노드의 ID, 이미 tree에 해당 ID에 해당하는 node의 범위에 대한 값이 있으면 그걸 바로 리턴할때 사용
nodeL: 현재 노드에서 커버하고 있는 범위의 맨 왼쪽
nodeR: 현재 노드에서 커버하고 있는 범위의 맨 오른쪽

고급

세그먼트 트리의 Item 데이터가 변경되는 경우, 세그먼트 트리를 업데이트 하는 함수

public static void update(int nodeId, int nodeL, int nodeR, int itemIndex, long itemValueDiff) {
    // 현재 노드의 범위를 벋어나면, 업데이트 할 필요 없음
    if (nodeL > itemIndex || nodeR < itemIndex) {
        return;
    } else {
        // 포함 범위면 갱신
        tree[nodeId] += itemValueDiff;

        // Leaf 노드가 아니면, 자식 노드 왼쪽, 오른쪽 역시 갱신
        if (nodeL != nodeR) {
            int mid =  (nodeL + nodeR) / 2;
            update(node * 2, nodeL, mid, itemIndex, itemValueDiff);
            update(node * 2 + 1, mid + 1, nodeR, itemIndex, itemValueDiff);
        }
    }
}

세그먼트 트리의 Item을 범위로 한번에 업데이트 하는 함수

public static int updateRangeValue(int nodeId, int nodeL, int nodeR, int L, int R) {
    if (R < nodeL || L > nodeR) {
        return 0;
    }

    if (nodeL == nodeR) {
        int diff = tree[nodeId];
        tree[nodeId] = 0;
        return diff;
    }

    int mid = (nodeL + nodeR) / 2;
    int ldiff = updateRangeValue((nodeId * 2), nodeL, mid, L, R);
    int rdiff = updateRangeValue((nodeId * 2 + 1), mid + 1, nodeR, L, R);
    int diff = ldiff + rdiff;
    tree[nodeId] = tree[nodeId] - diff;
    return diff;
}

세그먼트 트리를 Lazy Propagation 하는 방법

// tree와 동일한 크기의 lazy 배이 있어야 합니다.
public static int lazy [] = new int [ItemTotalNumber * 4];

public static void updateLazy(int nodeId, int nodeL, int nodeR) {
    // 업데이트할 부분이 있으면
    if (lazy[nodeId] != 0) {
        // 한번에 tree에다가 lazy 업데이트 해야 하는 부분을 실제 업데이트 합니다.
        tree[nodeId] += (nodeR - nodeL + 1) * lazy[nodeId];

        // leaf노드가 아니면, lazy 업데이트 정보를 propagation합니다.
        if (nodeL != nodeR) {
            lazy[nodeId * 2] += lazy[nodeId];
            lazy[nodeId * 2 + 1] += lazy[nodeId];
        }

        // 현재 lazy에 해당하는 node는 업데이트 했으니깐 재초기화 합니다.
        lazy[nodeId] = 0;
    }
}


// 위의 updateLazy을 호출하는 함수는 query와 updateRange가 됩니다.
public static int query(int nodeId, int nodeL, int nodeR, int L, int R) {
    // query할때, 아직 업데이트 안한게 있을 수 있으니, 업데이트 하고 값을 달라고 하면 됩니다.
    updateLazy(nodeId, nodeL, nodeR);
    if (L > nodeR || R < nodeL) {
        return 0;
    }

    if (L <= nodeL && R >= nodeR) {
        return tree[nodeId];
    }

    int mid = (nodeL + nodeR) / 2;
    return query(nodeId * 2, nodeL, mid, L, R) + query(nodeId * 2 + 1, mid + 1, nodeR, L, R);
}

public static void updateRange(int nodeId, int nodeL, int nodeR, int L, int R, int diff) {
    // 구간을 업데이트 하는 경우역시, lazy 업데이트는 현재 nodeId에 속하는 node만 딱 update하니
    // lazy 업데이트할꺼 있으면 먼저 하라고 합니다.
    updateLazy(nodeId, nodeL, nodeR);
    if (L > nodeR || R < nodeL) {
        return;
    }

    // 실질적으로는(보통은...) query 하기전에, update을 합니다.
    // 따라서, 현재 최상위 업데이트가 필요한 노드는 먼저 업데이트 하고,
    // 자식 요소들을 lazy하게 업데이트 가능하게 합니다.
    if (L <= nodeL && R >= nodeR) {
        tree[nodeId] += (nodeR - nodeL + 1) * diff;
        if (nodeL != nodeR) {
            lazy[nodeId * 2] += diff;
            lazy[nodeId * 2 + 1] += diff;
        }
        return;
    }

    int mid = (nodeL + nodeR) / 2;
    updateRange(nodeId * 2, nodeL, mid, L, R, diff);
    updateRange(nodeId * 2 + 1, mid + 1, nodeR, L, R, diff);
    tree[node] = tree[nodeId * 2] + tree[nodeId * 2 + 1];
}

세그먼트 트리에서 N번째 item이 들어있는 index 찾기

    public static int findN(int nodeId, int nodeL, int nodeR, int N) {
        if (nodeL == nodeR) {
            return nodeL;
        }
        int mid = (nodeL + nodeR) / 2;
        int l = queryTree(nodeId * 2, nodeL, mid, nodeL, mid);
        if (l >= N) {
            return findN(nodeId * 2, nodeL, mid, N);
        } else {
            int newN = N - l;
            return findN(nodeId * 2 + 1, mid + 1, nodeR, newN);
        }
    }

참고

http://blog.naver.com/PostView.nhn?blogId=kks227&logNo=220791986409

https://www.acmicpc.net/blog/view/9

세그먼트 트리(Segment Tree)