네트워크 유량(Network Flow)

Source(시작점) → Sink(도착점) 으로동시에 보낼 수 있는,데이터나 사물의 최대 양을 구하는 알고리즘, (커플매칭, 축사 소 보내기 등의 문제에 적합)

(즉 기존, 최단 거리와 같이 가장 적은 비용을 가지는 경로를 구하거나, 최단 비용을 구하는게 아님)

전체적으로 개념을 이해할때, network의 bandwidth로 대입하면서 생각하는게 좋다.

용어 정리

• Source: 시작점
• Sink: 도착점
• Capacity: 용량 (간선에서 소화 가능한 최대 양 or 값)
• Flow: 유량 (간선에서 용량을 점유하고 있는, 사용하고있는 양 or 값)
• c(a, b): 정점 a 에서 b로, 소화 가능한(남은) 용량 값
• f(a, b): 정점 a 에서 b로, 사용하고 있는(쓴) 유량 값

주의: 이제 간선의 값은, 비용이 아니라, 용량! 이 된다. 그리고, 해당 용량을 점유하는것(사용하는것)을 유량 이라고 표현한다.

개념 설명

네트워크 유량의 특징 3가지

1. 용량의 제한
   1. 각 간선에 흐르는 유량은 그 간선의 용량을 넘을 수 없다.
   2. f(a, b) <= c(a, b)

2. 유량의 보존

   1. 어떤 정점을 기준으로 보았을때, 해당 정점에 (들어오는 유량의 총 합 == 나가는 유량의 총합) 이여야 한다.

      • e.g) a - b - c, f(a, b) == f(b, c)

      • 위의 식은, 이해를 위한 단순 한줄 연결이고, 실제는 a-b, a-d, a-f 와 같이 복잡한 형태가 되기 때문에

        • Σf(source, x) = Σf(x, sink), x is conneted nodes

3. 유량의 대칭

   1. 이 개념이 네트워크 유량 알고리즘의 핵심 아이디어 이다.

   2. 정점을 네트워크 공유기(혹은 스위치 등)으로 생각하면, upload, download가 발생 가능하기 때문에 역방향이 생길수 있다는 의미의 이해가 조금이나마 도움이 된다.

   3. 이 개념의 사용을 보면서 이해를 높이는게 좋기 때문에 아래 추가적인 알고리즘 설명에서 이해를 높이고 여기서는 이런 특징이 있다고 알아두자

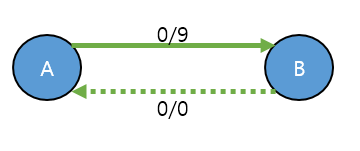
   4. 간선 a → b 가 있고, a → b의 capacity가 5 라면, b → a 라는 가상의 간선이 있고, 해당 간선의 capacity는 0 이라고 가정하는 것.

      • 이게 되는 이유는, 실제 b → a 는 없기 때문에 capacity 을 0 (허수)로 주어서 가상의 간선을 만든것

      • 즉, 1 + 2 = 3, 1 + 2 + 0 + 0 + 0 + 0 = 3, 0은 허수이기때문에 가상의 간선을 생성해도 논리적으로, 실제 결과에 영향이 없음

      • f(a, b) = -f(b, a)

알고리즘 설명

네트워크 유량의 가장 기본적인 알고리즘은, 포드 풀커슨(Ford-Fulkerson) 알고리즘과, 에드몬트 카프(Edmonds-Karp) 알고리즘 이 있습니다.

기본적으로 두개의 알고리즘은, brute force algorithm의 특성을 가집니다. 두 알고리즘 모두 아래와 같은 형태의 동작 원리를 가지게 됩니다.

1. Source에서 SInk로 가는 경로를 하나 찾습니다. (정식 용어로, 증가경로 augmenting path)
   • 이때 해당 경로는 반드시 여유 용량이 남아 있어야 합니다. 즉 c(a, b) - f(a, b) > 0

2. 찾아낸 경로에 보낼수 있는 최대 flow을 찾습니다. 보낼수 있는 최대 flow는 경로에 남은 capacity의 최소값입니다.

   • 현재 찾아낸 경로에서 보낼수 있는 가는한 최대의 flow 값(유량값)은, 경로에 남은 capacity의 최소값이 됩니다. 즉 경로상 Min(c(a, b) - f(a, b))

3. 찾아낸 경로에, 찾아낸 최대 flow을 실제 흘려보냅니다. (사용합니다)

   • 전체 경로에 f(a, b) += flow 을 하게 됩니다.

     • e.g) a - b - c - d 와 같은 경로라면, f(a, b) += flow, f(b, c) += flow, f(c, d) += flow 을 해줍니다.

   • 동시에 '유량의 대칭' 조건에 따라서, 역방향 역시 flow을 음수값으로 흘려 보냅니다.

     • e.g) a - b - c - d 와 같은 경로라면, f(b, a) -= flow, f(c, b) -= flow, f(d, c) -= flow 을 해줍니다.

     • 이게 되는 이유는, 가상의 역방향 간선의 capacity는 사실 0 이고, 해당 capacity에 - 값으로 flow(유량)을 흘려도, 용량의 제한 조건을 넘지 않습니다.

     • f(b, a) -= flow 일때, 즉 -1(flow) / 0(capacity) 형태이고, 이는 c(b, a) - f(b, a) > 0, (0 - (-1)) = 1이니깐. 조건을 만족합니다.

4. 1번에 해당하는 경로 찾기가 실패하기 전까지 위 1 ~ 3 번을 반복합니다.

그림으로 이해하기

아래와 같은 그래프가 그래프가 있을때 S(Source) → T(Sink)로 보내는 최대 유량, 위에서 설명한 알고리즘 설명 방식으로 구해 봅시다.

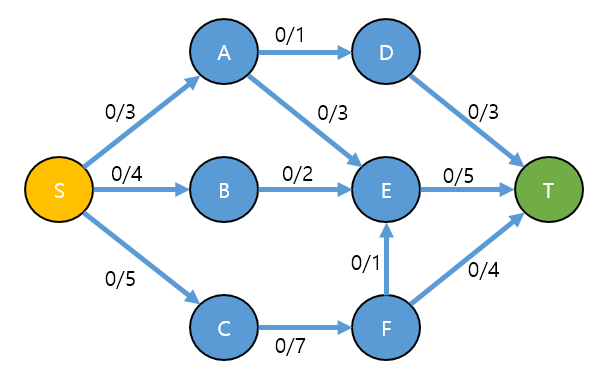
1. 증가경로(augmenting path)를 찾습니다

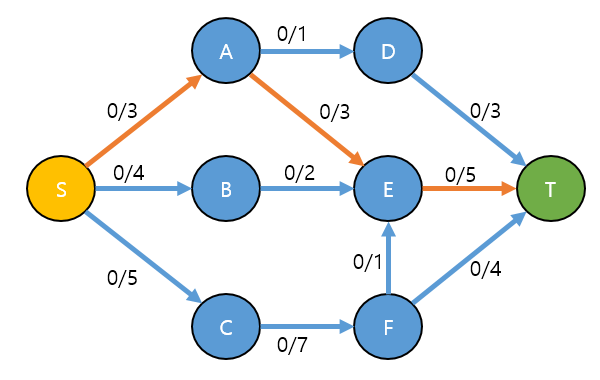
S → A → E → T 경로를 찾았습니다.

여기서는 역방향에 대한 개념 이해을 위해서 S → A → E → T을 처음 경로로 설정했다고 가정합니다.

• 경로를 찾는 법칙은 존재 하지 않습니다. (즉 S → B → E → T 도 되고, S → C → F → T 도 됩니다)
  • 단 경로를 찾을 때 반드시'경로는 반드시 여유 용량이 남아 있어야 합니다. 즉 c(a, b) - f(a, b) > 0'
  • 즉 경로에 여유 용량이 남아있으면 어떤 경로를 먼저 찾느냐에 대한 법칙은 없습니다.
• 보통은, 경로를 찾는부분을 DFS 또는 BFS로 하게 되고, 노드 ID(보통 0 ~ N) 순서로 탐색하게 되니.
  • 일반적으로는 (DFS를 썻다면, S → A → D → T 가 가장 먼저 경로로 나옵니다)
  • 여기서는 개념을 설명하는 부분이기 때문에 처음 경로를 S → A → E → T로 찾았다고 가정합니다.
• 경로를 찾았다의 조건은
  • Source → Sink 까지 도달해야 합니다.
  • 경로상에 여유 용량이 있어야 합니다.

2. 찾아낸 경로에 보낼수 있는 최대 flow을 찾습니다.

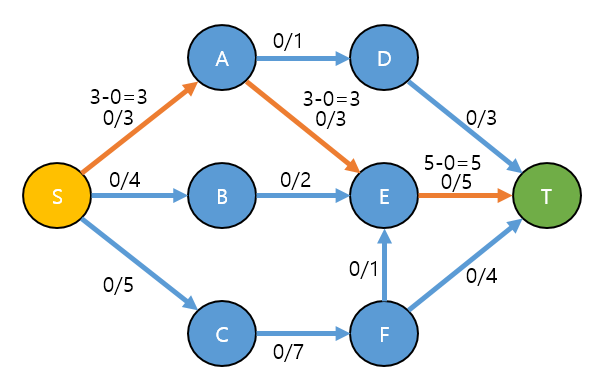
경로에서 보낼 수 있는 최대 flow는 각각의 구간에 남은 capacity의 최소값(min) 입니다.

S → A → E → T 에서 각각의 남은 capacity는 아래와 같습니다. (남은 capacity => c(a, b) - f(a, b))

• S → A: c(s, a) - f(s, a) = 3 - 0 = 3
• A → E: c(a, e) - f(a, e) = 3 - 0 = 3
• E → T: c(e, t) - f(e, t) = 5 - 0 = 5
• 위 3가지 경우에서 min 은 3 입니다.

3. 찾아낸 경로에, 찾아낸 최대 flow을 실제 흘려보냅니다. (사용합니다)

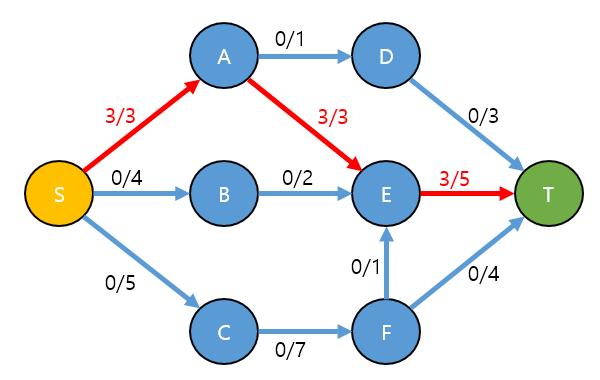
S → A → E → T 경로에 2번 과정에서 찾은 3을 흘려보냅니다(사용합니다)

현재 T까지 도달한 Total유량은 3입니다.

1 → 3 다시 반복. 이제 다시 1번 ~ 3번 과정을 반복합니다. 종료조건은 1번 (증가경로)를 더이상 찾지 못하는 경우가 됩니다.

S → B → E → T 경로를 찾고.

• S → B → E → T 의 최대 Flow값 == Min(c(a,b) - f(a,b)) 인 2를 찾고.
• S → B → E → T 에 2를 실제 흘려 보냅니다.

현재 T 까지 도달한 Total유량은 5입니다.

1 → 3 다시 반복. 이제 다시 1번 ~ 3번 과정을 반복합니다. 종료조건은 1번 (증가경로)를 더이상 찾지 못하는 경우가 됩니다.

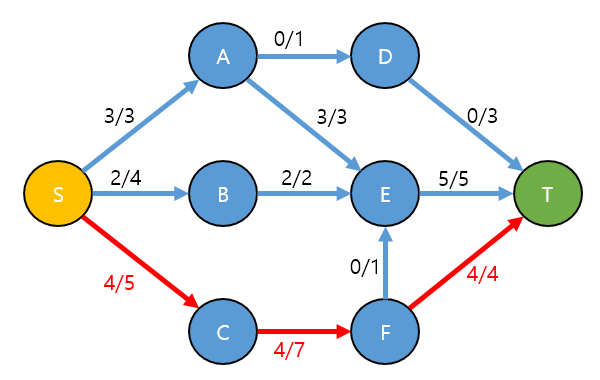
S → C → F → T 경로를 찾고

• S → C → F → T 경로의 최대 Flow값 == Min(c(a,b) - f(a,b)) 인 4를 찾고
• S → C → F → T 경로에 4를 실제 흘려 보냅니다.

현재 T 까지 도달한 Total유량은 9 입니다.

1 → 3 다시 반복. 이제 다시 1번 ~ 3번 과정을 반복합니다. 종료조건은 1번 (증가경로)를 더이상 찾지 못하는 경우가 됩니다.

1번 (증가경로) 를 더이상 찾을 수 없습니다.

현재까지 방법으로 얻은 답은, T 까지 도달한 Total유량은 9 가 됩니다.

하지만 9가 정말 답일까요???

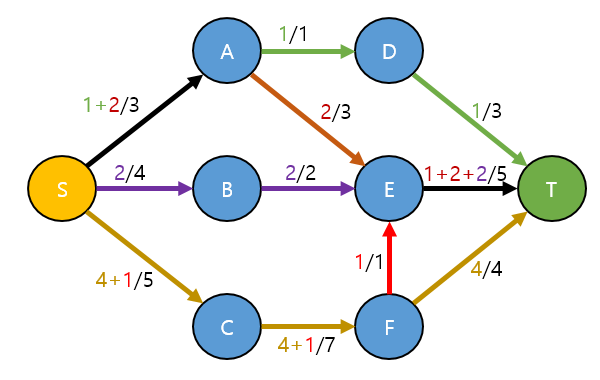
S → A → D → T 로 1

S → A → E → T 로 2

S → B → E → T 로 2

S → C → F → T 로 4

S → C → F → E → T 로 1

하면 Total 유량이 10 이 나오게 됩니다.

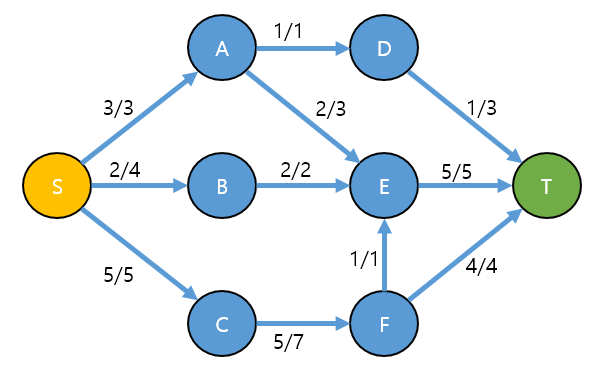
실제 정답과, 우리의 오답을 비교해 봅시다.

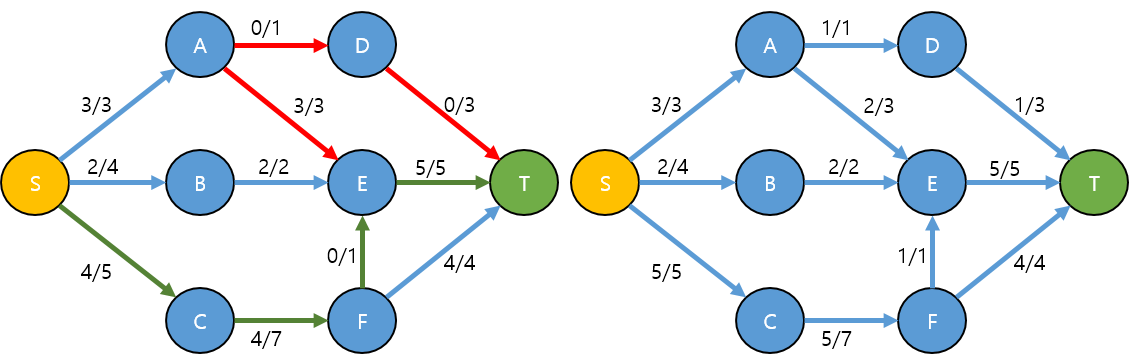
실제 정답과, 오답을 비교해보면

• S → A 로 흐르는 3 이라는 유량이 A → E 로 전부 3으로 흐르는 것이 아니라. A → D로 1 흐르고, A → E 로 2가 흐름을 알 수 있습니다.
• 따라서 A → E → T 가 1만큼의 여유분이 생기고.
• 해당 여유분 만큼 S → C → F → E → T 을통해 1이 흐르게 됩니다.

우리의 오답이 정답이 나오게 하려면.

• 처음 우리가 구한 A → E 유량 3을, 2가 되게 하고.
• 남는 유량 1을 A → E → T 의 path로 흐르게 하면 됩니다.

어떻게 해야 이런식으로 흐름을 조정 할 수 있을까요?

이를 가능하게 하는 아이디어가 가상의 간선(역간선)이 있다고 가정하는 것입니다. 결국 네트워크 유량의 포드 풀커슨 알고리즘과, 에드몬드 카프 알고리즘의 핵심은 이 가상의 간선(역간선)의 존재를 이용하는 것입니다.

역간선이 있는 상태에서, 1 → 3 다시 반복 해봅시다. 이제 다시 1번 ~ 3번 과정을 반복합니다. 종료조건은 1번 (증가경로)를 더이상 찾지 못하는 경우가 됩니다.

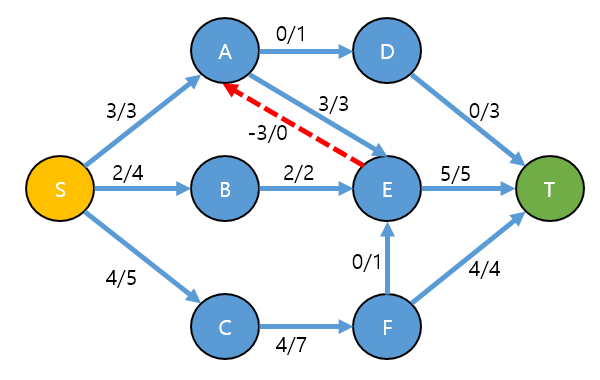
역간선이 있다면 다음과 같은 증가 경로를 찾을 수 있습니다.

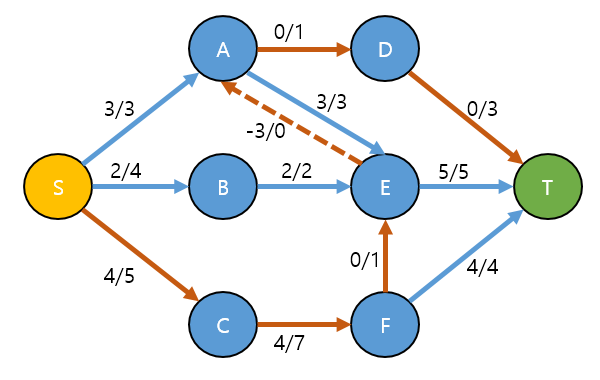
• 증가경로: S → C → F → E → A → D → T

• 경로의 각 부분은 아래와 같이 됩니다.

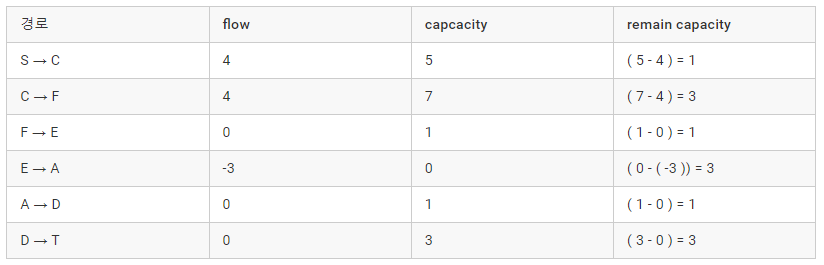
• 역방향 간선인 E → A는 3이라는 용량을 흘릴 수 있습니다.

증가경로를 찾았다면, 흘릴수 있는 최대 flow (Min(c(a,b) - f(a,b)) 즉 남은용량중 제일 작은값을 찾습니다.

• 여기서는 S → C, F → E, A → D 가 1 로 Min 값이고, flow는 1이됩니다.

증가경로와, 흘릴수 있는 최대 flow값을 구하였으니, 해당 경로에 flow을 흘려 보냅니다.

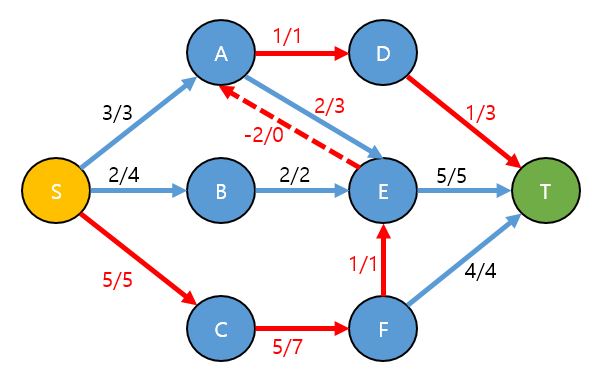
• 경로에 flow을 흘릴때, 정방향은 flow을 + 하고, 역방향은 - 하는걸 볼 수 있습니다.
  • f(a, b) += flow
  • f(b, a) -= flow
• flow을 정, 역방향을 흘림으로 해서, 기존 A → E가 2로 줄어들고, 1만큼 남은 내용이 A → D → T 로 가게 됨을 볼 수 있습니다.

역간선이 있는 상태에서, 1 → 3 다시 반복 해봅시다. 이제 다시 1번 ~ 3번 과정을 반복합니다. 종료조건은 1번 (증가경로)를 더이상 찾지 못하는 경우가 됩니다.

1번 (증가경로) 를 더이상 찾을 수 없습니다. (역간선이 있음에도!)

현재까지 방법으로 얻은 답은, T 까지 도달한 Total유량은 10 가 됩니다.

중간 정리

가상의 간선(역방향간선)을 이용해서, 최종적으로 우리가 원하는 최대의 유량을 구할 수 있음을 알 수 있습니다.

사실상 역방향 간선을 이해하면, 전체적인 흐름은,brute force algorithm의 특성을 가지기 때문에 이해하기 쉽습니다.

코드로 만들어 보기

지금까지 설명한 내용을 토대로 코드를 작성해 보도록 하겠습니다. 실제 구현이 아닌 이해를 위한 수도 코드 형태로 작성해 봅니다.

// 1. Source에서 SInk로 가는 경로를 하나 찾습니다.


public static Path findPath() {
    // dfs or bfs
    // c(a, b) - f(a, b) > 0 조건에 따라서 path을 찾을 수 있게 함.
}

// 2. 찾아낸 경로에 보낼수 있는 최대 flow을 찾습니다.


Path path = findPath();
FlowVal f;
for (p in path) {
  FlowVal pathFlow = p.capacity - p.flow;
  f = Math.min(f, pathFlow)
}

// 3. 찾아낸 경로에 실제 flow을 흘려보냅니다.


for (p in path) {
    path(a,b).flow += f; // 순방향에는 + 로 흘려줍니다.
    path(b,a).flow -= f; // 역방향에는 - 로 흘려줍니다.
}

최종적으로 아래와 같은 수도 코드를 만들 수 있습니다.

// 1 ~ 3  작업을 반복 합니다. 종료조건은, 1번 증가경로를 못찾는 경우까지


public static Path findPath() {
    // dfs or bfs
    // c(a, b) - f(a, b) > 0 조건에 따라서 path을 찾을 수 있게 함.
}


getMaxTotalFlow() {
    total = 0;
    while( (path = findPath()) != null ) { // 1. 경로 찾기 및 반복
        // 2. flow값 찾기
        FlowVal f;
        for (p in path) {
          FlowVal pathFlow = p.capacity - p.flow;
          f = Math.min(f, pathFlow)
        }


        // 3. flow 흘리기
        for (p in path) {
            path(a,b).flow += f; // 순방향에는 + 로 흘려줍니다.
            path(b,a).flow -= f; // 역방향에는 - 로 흘려줍니다.
        }


        total += flow;
    }


    // total 이 최대 유량이 됩니다.
    return total;
}

그래프 알고리즘에서 경로를 찾는 방법은 여러가지가 있지만, 가장 기본적인 경로 찾기 알고리즘으로 DFS와 BFS가 있습니다.

지금까지 설명한, 네트워크 유량 알고리즘의 경로 찾기 구현을, DFS로 하는 경우를 포드-풀커슨 알고리즘 이라고 하고, BFS로 하는 경우 에드몬트 카프 알고리즘 이라고 합니다.

• 포드-풀커슨: DFS
  • O(V + E) F)
• 에드몬드카프: BFS
  • O(VE^2)

두 알고리즘은 시간복잡도에서 차이가 납니다. 포드-폴커슨의 worst-case로 해당 내용을 좀더 살펴보겠습니다.

포드 풀커슨 최악의 케이스

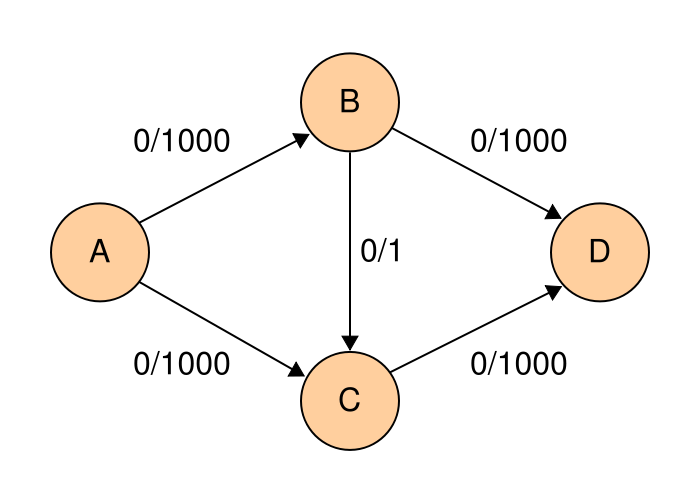
위와 같은 그래프가 있다고 가정합니다.

이때 네트워크 알고리즘을 사용하되, 포드-폴커슨을 구현했다고 봅니다.

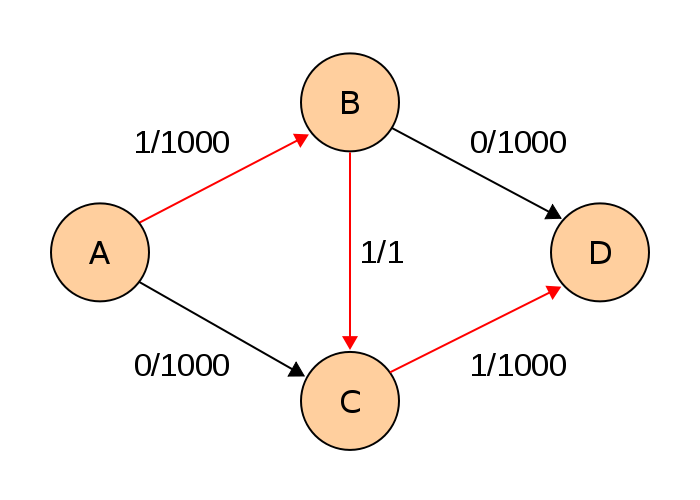
처음 A -> B -> C -> D 경로를 찾고, flow1을 흘려보냅니다.

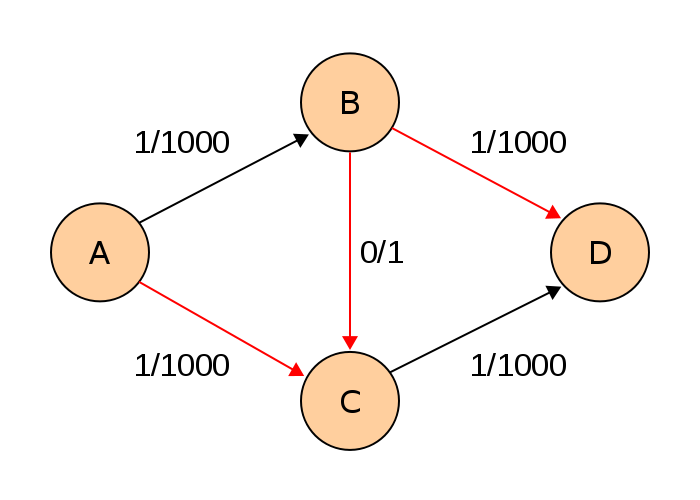
역간선을 이용해서 A -> C -> B -> D 의 경로가 찾아집니다.

DFS구현상 A -> B -> C에서 막히고, A -> C -> B -> D의 경로가 찾아지겠지요.

이제 A -> C -> B -> D로 flow 1을 흘려 보냅니다. B -> C 는 역간선 C -> B에 flow가 흐를때 -1되어 0/1로 초기화 되었습니다.

그럼 이제 다시 처음 A -> B -> C -> D의 경로가 됩니다.

결국 1000번의 루프를 타게 되고

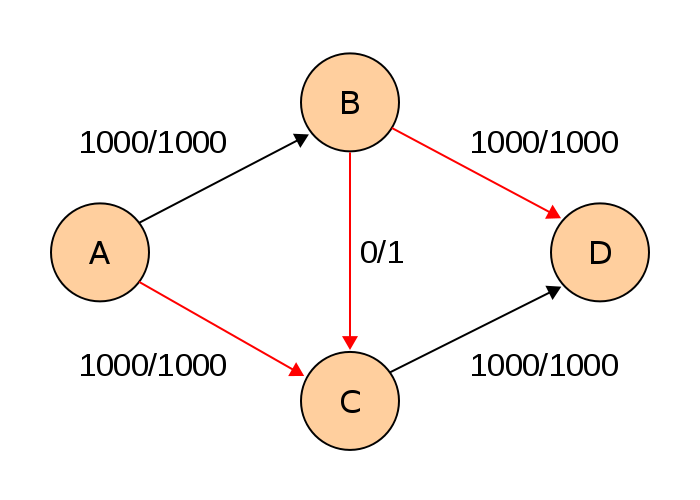
최종 답이 나오게 됩니다.

결국 포드-풀커슨 형태로 경로를 탐색하게 되면, 최악의 경우 flow의 max수치 (위 예제에서는, 1000)만큼 루프를 반복하게 됩니다.

시간복잡도가 결국, O(V+E)F 형태가 됩니다.

에드몬드-카프로, 포드-풀커슨 최악을 생각해보기

에드몬드-카프는, 포드-풀커슨 알고리즘과 전체 로직은 모두 동일하지만, 경로를 찾는 부분만 BFS형태를 취하게 됩니다.

위의 포드-풀커슨을 에드몬드-카프로 생각해 봅시다.

에드몬드-카프 BFS탐색

• 처음
  • A -> B -> C -> D, 처음 루프는 동일하게 됩니다.
• 두번째
  • 방문 A, 큐 [B, C] (A에서 방문 가능한 노드)
  • 방문 A, B, 큐 [C, (B에서 방문 가능한 노드 [C, D]], 그런데, B -> C는 1 /1 로 되어 있을테니, 큐 [C, D]
  • 방문 A, B, C, 큐[D, (C에서 방문 가능한 노드 [B, D]], 즉 [D, B, D]
  • 방문 A, B, C, D, 큐[B, D] 상태
  • 경로 A -> C(A로부터 방문) -> D(C로부터 방문) 찾음
  • A -> C -> D 이기 때문에 포드 풀커슨과 달리, B -> C 역방향 간선 flow update에 따른 B -> C 간선 capacity초기화 없음.

보다싶인 에드몬드-카프 방식(BFS)로 탐색을 하면, flow보다는 edge에 영향을 받게 됩니다. 따라서 flow에 영향을 받는 포드-풀커슨과 달리 시간복잡도가, O(VE^2) 형태가 됩니다.

이론 핵심 요약

• Source(시작점) → Sink(도착점) 으로동시에 보낼 수 있는,데이터나 사물의 최대 양을 구하는 알고리즘
• 복잡도
  • 포드-풀커슨: O(V+E)F
  • 에드몬드카프: O(VE^2)
• 주의
  • 일부 블로그 설명에서, 포드-풀커슨의 문제점 때문에 '에드몬드카프'가 좋다고 되어 있는데, 무조건 좋은게 아니라 문제에 따라서 취사 선택해야합니다!
  • 문제에 Flow값이 적고, Edge가 많으면 오히려 에드몬드카프가 더 느릴 수 있습니다.

• 알고리즘 핵심

  1. Source에서 Sink로 가는 경로를 하나 찾습니다. (정식 용어로, 증가경로 augmenting path)

  2. 찾아낸 경로에 보낼 수 있는 최대 flow을 찾는다.

  3. 찾아낸 경로에, 찾아낸 최대 flow을 흘려보낸다. (사용한다.)

  4. Source -> Sink 경로를 찾지 못할때 까지 반복한다.

구현 핵심 요약

Java로 설명한다

필요한 요소

• 그래프를 표현한 자료구조 (LinkedList | ArrayList | Array[][])
• path을 저장하기위한 자료구조 (Array[])
• edge(간선)의 정보를 저장하기 위한 자료구조
  • capacity (Array[][])
  • flow (Array[][])
• dfs에서 방문 정보를 확인하기 위한 자료구조 (Array[])

코드

    public static int capacity[][];
    public static int flow[][];
    public static int path[]; // 
    public static boolean visited[];
    public static LinkedList<Integer> graph[];

    public static boolean dfs(int start) {
        if (start == Sink) {
            return true;
        }

        visited[start] = true;
        LinkedList<Integer> nexts = graph[start];
        for (int next: nexts) {
            if ( !visited[next] && capacity[start][next] - flow[start][next] > 0) {
                path[next] = start;

                if (dfs(next)) { // 경로를 끝까지 찾으면 탈출, 아니면, 끝까지 찾기 재시도
                    return true;
                }
            }
        }
        return false;
    }

    public static boolean bfs() {
        Arrays.fill(path, -1);
        Queue<Integer> q = new LinkedList<Integer>();
        q.add(Source);

        while (!q.isEmpty()) {
            int from = q.poll();
            LinkedList<Integer> nexts = graph[from];

            for (int next: nexts) {
                if ( path[next] == -1 && (capacity[from][next] - flow[from][next]) > 0 ) {
                    path[next] = from;
                    q.add(next);

                    if (next == Sink) {
                        break;
                    }
                }
            }
        }

        if (path[Sink] == -1) {
            return false;
        }

        return true;
    }

    // O(VE^2)
    public static int EdmondsKarp() {
        int total = 0;
        while (bfs()) {
            // flow값 찾기
            int flowNum = Integer.MAX_VALUE;
            for(int i = Sink; i != Source; i = path[i]) {
                int from = path[i];
                int to = i;
                flowNum = Math.min(flowNum, (capacity[from][to]) - flow[from][to]);
            }

            // flow흘려 보내기, 역방향도 반드시!!!!
            for(int i = Sink; i != Source; i = path[i]) {
                int from = path[i];
                int to = i;

                flow[from][to] += flowNum;
                flow[to][from] -= flowNum;
            }

            total += flowNum;
        }
        return total;
    }

    // O((V+E)F)
    public static int FordFulkerson() {
        int total = 0;
        while (dfs(Source)) { // dfs로 경로 찾기(증가경로), 경로가 더이상 없으면 종료임.
            // 찾은 경로에서 차단 간선 찾기 min (capacity[u][v] - flow[u][v])
            // 결국 의미는 경로에서 흘릴수 있는 최대의 유량(flow)을 찾기
            int flowNum = Integer.MAX_VALUE;
            for(int i = Sink; i != Source; i = path[i]) {
                int from = path[i];
                int to = i;
                flowNum = Math.min(flowNum, (capacity[from][to]) - flow[from][to]);
            }
            // 찾은 경로에 유량을 흘려보내기, 역방향도 반드시!!!!
            for(int i = Sink; i != Source; i = path[i]) {
                int from = path[i];
                int to = i;

                flow[from][to] += flowNum;
                flow[to][from] -= flowNum;
            }

            total += flowNum;

            // 찾은 경로를 초기화해서 dfs로 경로 찾기를 Source > Sink 까지 다시 할 수 있게 함.
            Arrays.fill(path, -1);
            Arrays.fill(visited, false);
        }
        return total;
    }

조금 더 생각해 보기

만약 문제에서 역방향 간선 자체가 입력으로 주어진 경우는 어떻게 해야 하나?

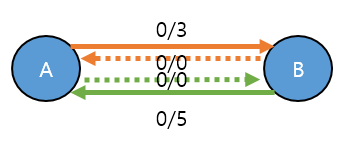
• A -> B, 3 B -> A, 5

위와 같은 형태로 입력값이 주어진다면, A -> B 입력에 대한 역방향 간선(허수 간선) B -> A가 용량 0으로 있어야 하는데, 실제 B -> A 입력 때문에 허수가 아닌 실제값을 가지는 간선 B -> A가 있게 됨.

역방향 간선은 허수값을 용량으로(capacity)가는 형태가 되어야 하는데, 문제 자체에서 반대 방향을 Input 으로 주어서 capacity가 실제 값을 가지는 형태가 된다. 그럼 최초와 같이 brute force algorithm 형태에서 못찾는 경로가 발생 할 수 있다.

어떻게 해야 할까?

이런경우는 가상의 정점을 하나 두고 해당, 정점을 거쳐서 가는 형태로 바꾸어 주면 된다.

네트워크 유량의 특성(용량의 제한, 유량의 보존)을 만족시키기 때문에 문제가 없다.

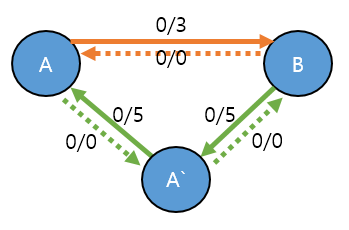
만약 문제에서 같은 방향의 간선이 여러개 입력으로 주어진 경우는?

• A -> B, 3 A -> B, 4 A -> B, 2

동일한 방향의 간선이라면, 사실 하나의 간선에, 용량을 모두 더해서 생각하면 된다.