펜윅 트리(Fenwick Tree, Binary Indexed Tree, BIT)
기본 개념 정리
세그먼트 트리의 메모리를 절약하기 위한 방법으로 만들어진 트리 이다.
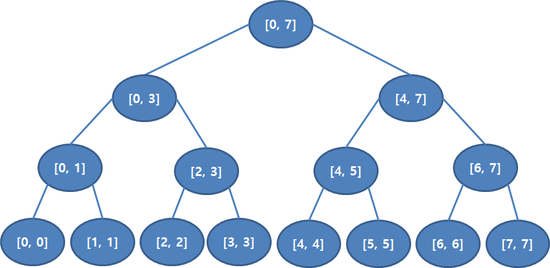
세그먼트 트리의 경우 Node가 전체 Item에 대한 범위가, 2진 형태의 부분 범위로 확장되는 모습을 가진다면,
펜윅 트리의 경우, 부분 범위 확장시 불필요한 정보를 제외한 형태로 확장되는 모습을 가진다.
| 세그먼트 트리 | 펜윅 트리 |
|---|---|
 |
 |
| L ~ R 범위 가져오기: getValue(L, R) | L ~ R 범위 가져오기: getValue(R) - getValue(L) + R value |
| 펜윅 트리는 1 ~ X 까지의 값을 가져오는 방법만 됨 |
펜윅 트리의 기본 아이디어
세그먼트 트리의 [0, 7]의 값과, [0, 3]의 값을 알고 있다면, 굳이 [4, 7]의 값을
유지할 필요가 없다. 왜냐하면, [0, 7]의 값 - [0, 3]을 하면, [4, 7]의 값을 알 수 있기 때문이다. 따라서 세그먼트 트리상의 우측 노드들을 유지 하지 않는 형태를 가진다.
세그먼트 트리를 공부하였다면, 펜윅 트리의 기본 아이디어 까지는 쉽게 이해가 가능하다.
하지만, 실제 펜윅 트리를 구현하는 방법, 특히 트리 초기화, 트리에 값을 갱신, 트리에서 구간 값을 가져오는
방법 등은 아이디어를 이해했다고 해도 쉽게 떠오르지 않을 수 있다. 해당 내용은 구현 핵심 요약에서 자세히
설명한다.
펜윅 트리 요약
미리 정리하자면, 세그먼트 트리와 펜윅 트리의 다른점은 결국 위에서 설명한 펜윅트리의 아이디어에서 기인하게 된다.
펜윅 트리는 세그먼트 트리와 달리, 불필요한 정보을 제외하고 있기때문에, 곧바로 어떤 구간에 대한
값을 곧바로 가져오지는 못한다. 즉 세그먼트 트리에서 getValue(L, R)와 같은형태로 값을 구하는데,
펜윅 트리에서는 항상 getValue(L)형태로 값을 구하게되고, 이는 1 ~ L, 즉 세그먼트 트리의 getValue(1, L) 형태와 같다.
따라서 펜윅 트리에서 L ~ R의 값을 얻기 위해서는, 1 ~ L = L', 1 ~ R = R'의 값을 얻고, R' - L' + L 와 같은 형태를
취해야만, L ~ R의 값을 얻을 수 있다.
이론 핵심 요약
어떤 구간의 값을 나타내는 알고리즘
- 트리의 요소 (Item)은 정해져 있고, 해당 요소의
범위(구간)에 대한 값(합, 차, 최소, 최대, 평균, .. 등등)을 구할 때 사용 트리를 바이너리 인덱스 형태로 만들어서 풀이한다.
- 트리의 크기는 결국 요소 (Item)의 크기와 동일한 형태로 만들어진다.
- (세그먼트 트리의 우측 구간 - 즉 1/2 씩 공간을 줄인다.)
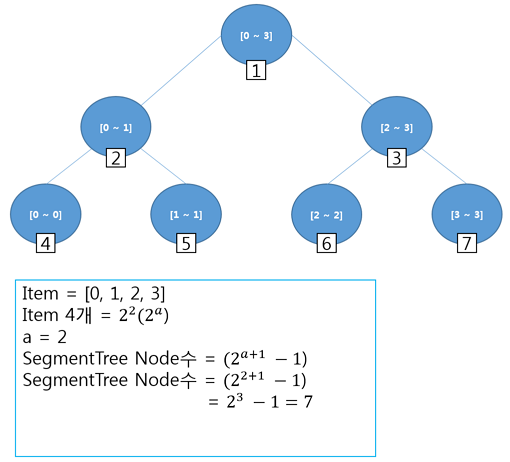
세그먼트 트리가 루트부터 Left, Right노드를 만들면서, Node에 ID을 순서대로 붙여가는 형태에 반해, 펜윅 트리는, 1부터 ~ N까지 (트리의 크기는 요소의 크기와 동일), ID가 고정되는 형태이다.
세그먼트 트리의 노드는 Level순회 형태로 ID를 부여한다.
펜윅 트리는 트리 순서대로 ID는 고정
| 세그먼트 트리 | 펜윅 트리 |
|---|---|
 |
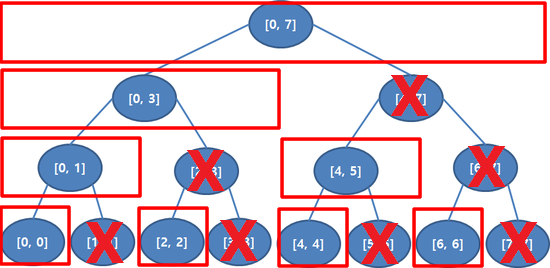 |
| 펜윅 트리, 트리 node index 모습 (위 그림을 단순히 표현) |
|---|
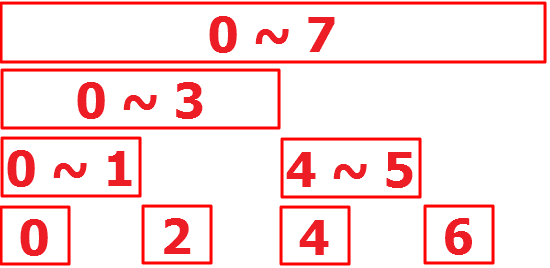 |
| 펜윅 트리, 트리 node index 모습 (인덱트를 1부터 시작하도록 표현) |
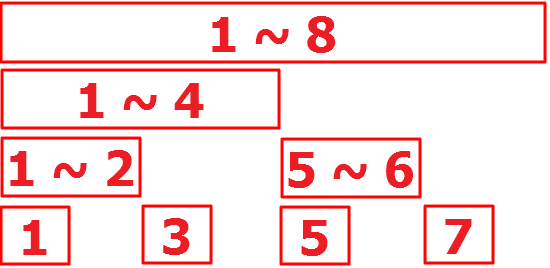 |
| 펜윅 트리, 트리 node index 모습 (실제 노드 인덱스에 들어가는 정보와 인덱스 형태) |
 |
펜윅 트리의 하나의 노드가 나타내는 값 중 알수 있는 정보는, 그노드가 나타내는 범위의 last index 이다.
- 펜윅 트리의 노드의 값은 자기자신을 수도 있고, 범위 값일 수도 있다. 또한 범위값의 시작점을 알기 힘들다.
- 세그먼트 트리가 루트(ID=1)(0 ~ N)범위, 루트의 L자식(ID=2)(0 ~ N/2), 루트의 R자식(ID=3)(N/2 ~ N) 형태로 확장되는 형태에 반해, 펜윅 트리는, 1(1), 2(1 ~ 2), 3(3), 4(1 ~ 4), ..., 12(9 ~ 12), ... 와 같이 어떤 노드는, 범위이고, 어떤 노드는, 범위가 아니고, 또한 어떤 노드는(1 ~4) 시작되고, 어떤 노드는 중간(9 ~ 12) 부터 시작된다. 이는 **펜윅 트리가. 바이너리 형태로 불필요 정보(정확하게는 세그먼트트리상의 우측 자식 정보)을 제외하고 정보를 저장**하고 있기 때문이다.
- 펜윅 트리에서 트리의 Index(Node ID) 정보를 통해서 알 수 있는 것은, 해당 노드가, ? ~ Index 까지의 정보 를 담고 있다는 사실이다. 즉, 펜윅 트리의 18번 Node는 ? ~ 18 까지의 정보를 담고 있다. 같은 의미로, 어떤 범위의 last Index을 알수 있다.
복잡도 O(Log N)
- 업데이트나, 값 구하기 모두 O(LogN)으로 동작한다.
- 세그먼트 트리에 비해서, 메모리를 적게 먹고, 업데이트가 자주 일어나는 동작에 좀더 유리하다.
- 없데이트나, 값 구하기 시, 루프문 하나를 반복할때마다. Tree의 depth을 하나 올라간다고 보면된다.
구현 핵심 요약
Java로 설명한다.
필요한 요소
- 문제에서 주어지는 Item을 저장하는 자료구조 (Array | List) - e.g)
int [] items - 펜윅 트리를 표현하는 자료구조 (Array | List | Map) - e.g)
int [] tree - 펜윅 트리에서 N index의 값을 업데이트 하는 함수
- 펜윅 트리에서 1 ~ N 까지의 구간값을 구하는 함수
코드
펜윅 트리의 생성
펜윅 트리는 item 의 수와 동일하기 때문에 item 수만 알면 곧바로 생성 가능하다.
주의 할 점은 index로 돌기때문에 0 인덱스는 버리고 1 부터 진행하게 한다. 따라서 +1 형태로 트리를 생성하면 된다.
트리 생성 하기(item이 N개 일때)
public static int tree[];
...
tree = new int[N + 1];
펜윅 트리에서 N index의 값을 업데이트 하는 함수
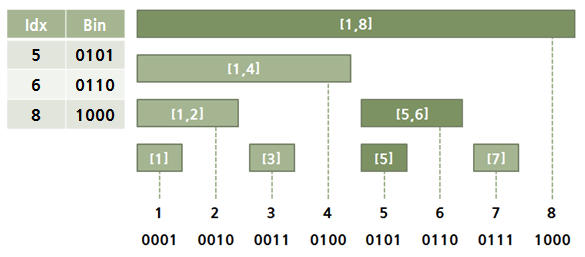
- N index는 1 <= N <= 문제에서 주어지는 item.size 가 된다. (펜윅 트리 크기 === 문제에서 주어지는 item 수)
- N index의 값을 업데이트 하면, N index와 연관된 펜윅 트리 노드를 같이 update해야 한다.
- e.g) 총 item 8개일때, update(5, value) 하면 ==> 5, 6, 8번 노드에 업데이트가 돌아야함 - 위 그림 참고
- 펜윅 트리의 5, 6, 8 번 노드의 index을 바이너리 형태로 만들면 다음과 같다. (펜윅 트리를 바이너리 인덱스 트리로 부르기도 함)
- 5(0101) > 6(0110) > 8(1000)
- 5(0101) + 0001 = 6(0110)
- 6(0110) + 0010 = 8(1000)
- 결국 N index을 업데이트 할때, 연관된 트리 노드는 N index을 바이너리로 봤을때 맨 마지막 1이 나오는 bit을 찾아서 더하는 형태가 된다.
- 5(0101) > 6(0110) > 8(1000)
- 쉽게 외우기
- 펜윅 트리에서 업데이트는 업데이트 하려는 index와 관련된 인덱스가 모두 업데이트 되어야 한다.
- 가장 오른쪽 1 비트 구하기:
index & -index - 모두 업데트니니깐, + 형태:
index += (index & -index) - 루프는 점점 index가 더해지는 형태니깐 tree size보다 작을때까지:
while (index < tree.length)
트리의 N index의 값을 업데이트 하기 (예제 구간의 합)
public static int tree[];
/**
* @param index
* 펜윅 트리의 업데이트 에서 index는 펜윅 트리 내부적으로 관리하고 있는 노드의 값중
* 해당 index와 연관 있는 노드의 값들을 모두 업데이트 하라는 의미가 된다.
* 따라서 업데이트가 성공적으로 이루어 지고 나면, index와 관련된 노드 값이 모두 업데이트 상태에서,
* 1 ~ N 까지의 값을 얻을 수 있다.
*
* @param diffValue
* diffValue을 주어야 하는 이유
* 펜윅 트리에서 업데이트는 index와 관련된 모든 노드의 값을 변경하게 된다.
* 이때, 업데이트가 발생하게 되는 노드들은, 범위를 나타낼 수 도 있고, 그냥 값을 나타낼 수도 있다.
* e.g) item이 총 8개일때, 5번째 item값을 update하는 경우
* 펜윅 트리 개념도로 보면, 5, 5~6, 1~8 (index가 5인것과 관련있는 node들)이 된다.
* 결국 위의 관련있는 노드는, 펙윅 트리의 5번 노드, 6번 노드, 8번 노드가 update된다.
* 이때, 5번 노드는 하나의 값만 표현(가지)고 있지만, 8번 노드는, 1~8의 범위에 대한 값을 가지게 된다.
* 따라서, 아래 update 함수에서, 5번 index에 대하여
* 기존 (10) 이라는 값이 있었고, 새로 (5)라는 값으로 변경된다고 가정하면,
* 범위값을 설정하는 경우를 위해서, 이전값 에서 새로 변경되는 값으 차이인 (-5) 값으로 5번 index와 관련된 모든
* 노드를 업데이트 하라고 해야 한다.
*
* 펜윅 트리에서 어떤 index을 주고, 값을 업데이트 시킬때,
* 해당 index와 연관된 노드는 2진수로 봤을때, 가장 오른쪽 1 위치에 +1 하는 형태이다.
* e.g) 5(0101) > 6(0110) > 8(1000)
*/
public static void update(int index, long diffValue) {
while (index < tree.length) {
tree[index] += diffValue; // 합을 구하는 경우니까.
/**
* java에서 음수는 2의 보수로 표현 (양수의 2의 보수 만들고 +1)
* e.g)
* 5: (00000000 00000000 00000000 00000101)
* 2의 보수 5: (11111111 11111111 11111111 11111010)
* -5: (11111111 11111111 11111111 11111011)
*
* -------------------------------------------------
* 5와 -5의 & 연산
* 5: (00000000 00000000 00000000 00000101)
* -5: (11111111 11111111 11111111 11111011)
* (00000000 00000000 00000000 00000001) 5의 가장 오른쪽 1
*
* 가장 오른쪽의 1 위치값을 (자기수 & -자기수) 연산으로 구했음. 따라서
* 펜윅 알고리즘상 다음 index구하기는, 가장 오른쪽 1 비트에 1 더하기 이니.
* 5: (00000000 00000000 00000000 00000101)
* + (00000000 00000000 00000000 00000001) 5의 가장 오른쪽 1
* -------------------------------------------------- 위 갑을 더하면
* 00000000 00000000 00000000 00000110 === 6 이 됨
*/
index += (index & -index);
}
}
펜윅 트리에서 1 ~ N 까지의 구간값을 구하는 함수
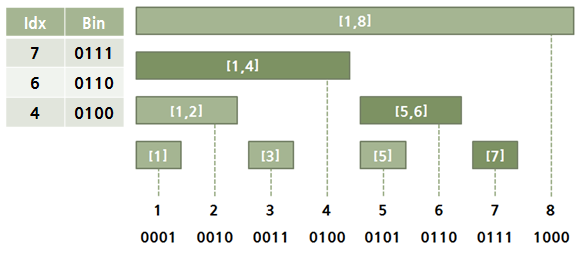
- 1 ~ N으로 시작 범위가 고정이기 떄문에 보통 N만 매개 변수로 받는다.
- 펜윅 트리 내부적으로는, 불필요한 정보가 빠져있기떄문에, 연관된 연속 정보값을 가져오는 형태가 되어야 한다.
- 연관된 연속 정보 값은, 결국 펜윅트리의 노드 어딘가에 정보가 있게 된다.
- e.g) getValue(7) 와 같이 N 이 7인 값을 get하는 경우 (이때 의미는 1 ~ 7 구간 값을 가져오겠다가 된다.)
- 이경우, 7번, 6번, 4번 노드의 값을 각각 가져와서 더해주어야 함. --> 위 그림 참고
- e.g) getValue(7) 와 같이 N 이 7인 값을 get하는 경우 (이때 의미는 1 ~ 7 구간 값을 가져오겠다가 된다.)
- 펜윅 트리의 7, 6, 4 번 노드의 index을 바이너리 형태로 만들면 다음과 같다.
- 7(0111) > 6(0110) > 4(0100)
- 7(0111) - 0001 = 6(0110)
- 6(0110) - 0010 = 4(0100)
- 7(0111) > 6(0110) > 4(0100)
- 쉽게 외우기
- 펜윅 트리에서 값 구하기는 구하려는 index와 관련 노드가 겹치지 않는 연속된 형태의 index 값을 구해야 함.
- 가장 오른쪽 1 비트 구하기:
index & -index - 겹치지 않는 index니깐 , - 형태:
index -= (index & -index) - 루프는 index가 점점 줄어드는 형태니깐 0보다 클때까지:
while(index > 0)
트리의 N index의 값 구하기 (예제 구간의 합, 1 ~ N까지의 값이 구해짐)
/**
* @param index
* 펙윈 트리에서는, 값을 get 할때 1 ~ index의 값을 리턴하는 형태로 되어 있다. (항상 1 ~ )이다.
* 세그먼트 트리와 다르게 (4 ~ 9) 이런 형태가 아니고 항상 (1 ~ index)형태이기 때문에
* 세그먼트 트리처럼 (a ~ b)의 구간값을 가져오기 위해서는 (1 ~ b) - (1 ~ a) + a형태로 사용하여야 한다.
*
* 펙윅 트리 내부 에서, 1 ~ index 의 값을 얻는 방법은, update와는 반대로, index와 관련되지는 않지만.
* index와 연속적으로 이어지는 node들 모두 모으면 되는 형태이다.
* update와 마찬가지로, 펜윅트리의 자료구조 자체가 어떤 노드는 범위이고, 어떤 노는는 범위가 아닌 상태가 될 수 있다.
* 따라서, index와 관련있는 node을 연속적으로 이을 수 있는 node을 찾는 과정이 필요하다.
*
* e.g) item이 총 8개일때, 1 ~ 7 범위 값을 get하는 경우.
* 펜윅 트리 개념도로 보면, 7, 5~6, 1~4 (index === last index가 7일때 연속 node)이 된다.
* 결국 위의 연속노드는, 펙윅 트리의 7번 노드, 6번 노드, 4번 노드가된다.
* 연속 노드들에 저장된 값을 모두 가져오면, 1 ~ 7 범위의 값을 get 할 수 있다.
*
* 펜윅 트리에서 1 ~ N 범위 값을 get할때, 주어지는 last index의 최하위 1비트가 0으로 변경되는 형태이다.
* 결국 가장 오른쪽 1인 값을 가져오는 것은 udpate와 동일하고, 기존값에서 - 형태를 취하면 된다.
* 7(111) > 6(110) > 4(100)
*/
public static long getOneToIndexRangeValue(int index) {
long result = 0;
while (index > 0) {
result += tree[index];
/**
* java에서 음수는 2의 보수로 표현 (양수의 2의 보수 만들고 +1)
* e.g)
* 7: (00000000 00000000 00000000 00000111)
* 2의 보수 7: (11111111 11111111 11111111 11111000)
* -7: (11111111 11111111 11111111 11111001)
*
* -------------------------------------------------
* 7와 -7의 & 연산 (가장 오른쪽 1 찾기)
* 7: (00000000 00000000 00000000 00000111)
* -7: (11111111 11111111 11111111 11111001)
* (00000000 00000000 00000000 00000001) 7의 가장 오른쪽 1
*
* 가장 오른쪽의 1 위치값을 (자기수 & -자기수) 연산으로 구했음. 따라서
* 펜윅 알고리즘상 다음 node의 index구하기는, 가장 오른쪽 1 비트에 1 빼기 이니.
* 7: (00000000 00000000 00000000 00000111)
* - (00000000 00000000 00000000 00000001) 7의 가장 오른쪽 1
* -------------------------------------------------- 위 갑을 빼면
* 00000000 00000000 00000000 00000110 === 6이 됨
*/
index -= (index & -index);
}
return result;
}
참고